Now that we have a definition of work, we can apply the concept to
kinematics. Just as force was related to
acceleration
through F = ma, so is work related to velocity through the Work-Energy
Theorem.
Derivation of the Work-Energy Theorem
It would be easy to simply state the theorem mathematically. However, an
examination of how the theorem was generated gives us a greater understanding of
the concepts underlying the equation. Because a complete derivation requires
calculus, we shall derive the theorem in the one-dimensional case with a
constant force.
Consider a particle acted upon by a force as it moves from xo to xf. Its
velocity also increases from vo to vf. The net work on the particle is
given by:
Wnet = Fnet(xf - xo)
Using Newton's Second Law we can
substitute for F:
Wnet = ma(xf - xo)
Given uniform acceleration,
vf2 - vI2 = 2a(xf - xo). Substituting for
a(xf - xo) into our work equation, we find that:
Wnet = 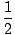 mvf2 - mvf2 - 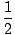 mvo2 mvo2 |
|
This equation is one form of the work-energy equation, and gives us a direct
relation between the net work done on a particle and that particle's velocity.
Given an initial velocity and the amount of work done on a particle, we can
calculate the final velocity. This is important for calculations within
kinematics, but is even more important for the study of energy, which we
shall see below.
Kinetic Energy and the Work-Energy Theorem
As is evident by the title of the theorem we are deriving, our ultimate goal is
to relate work and energy. This makes sense as both have the same units, and
the application of a force over a distance can be seen as the use of energy to
produce work. To complete the theorem we define kinetic energy as the
energy of motion of a particle. Taking into consideration the equation derived just previously, we define the kinetic energy
numerically as:
K = 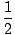 mv2 mv2 |
|
Thus we can substitute
K in our work energy theorem:
Wnet =
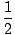 mvf2
mvf2 -
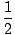 mvI2
mvI2 =
Kf -
Ko
Implying that
This is our complete Work-Energy theorem. It is powerfully simple, and gives us
a direct relation between net work and kinetic energy. Stated verbally, the
equations says that net work done by forces on a particle causes a change in the
kinetic energy of the particle.
Though the full applicability of the Work-Energy theorem cannot be seen until we
study the conservation of energy, we
can use the theorem now to calculate the velocity of a particle given a known force at any position.
This capability is useful, since it relates our derived concept of work back to
simple kinematics. A further study of the concept of energy, however, will
yield far greater uses for this important equation.