Problem :
In Solving the Orbits we derived the
equation:
From this, derive the expression we stated for
1/r. Hint: Define
y = 1/r
and use the fact that
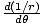 = -
= - 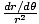
.
Making the
y substitution, we have:
We can then complete the square on the right-hand side and we have:
Then we let
p = y - 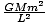
and we have:
where we have just defined
C in terms of the constant
E, G, M, m, L. We can
now separate variables:
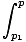 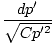 = = 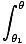 dθ'âá’cos-1(p'/ dθ'âá’cos-1(p'/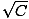 )|pp1 = θ - θ1âá’p = )|pp1 = θ - θ1âá’p = 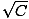 cos cos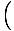 (θ - θ1) - cos-1(p1/ (θ - θ1) - cos-1(p1/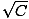 ) )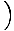 = = 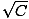 cos(θ - θ0) cos(θ - θ0) |
|
Finally, recalling
p = (1/r) - 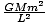
, and we can pick an axis such
that
θ0 = 0:
The quantity under the radical is defined a
ε, the eccentricity.
Problem :
Using the expression we derived for (1/r), show that this reduces to x2 = y2 = k2 -2kεx + ε2x2, where k = 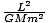 ,
ε =
,
ε =  , and cosθ = x/r.
, and cosθ = x/r.
We have:
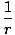 = = 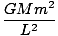 (1 + εcosθ)âá’1 = (1 + εcosθ)âá’1 = 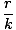 (1 + ε (1 + ε )âá’k = r + εx )âá’k = r + εx |
|
We can solve for
r and then use
r2 = x2 + y2:
which is the result we wanted.
Problem :
For 0 < ε < 1, use the above equation to derive the equation for an
elliptical orbit. What are the semi-major and semi-minor axis lengths? Where
are the foci?
We can rearrange the equation to
(1 - ε2)x2 +2kεx + y2 = k2. We can divide through by
(1 - ε2) and complete the square in x:
Rearranging this equation into the standard form for an ellipse we have:
 + +  = 1 = 1 |
|
This is an ellipse with one foci at the origin, the other at
(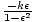 , 0)
, 0), semi-major axis length
a = 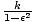
and semi-minor axis length
b = 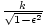
.
Problem :
What is the energy difference between a circular earth orbit of radius 7.0×103 kilometers and an elliptical earth orbit with apogee 5.8×103 kilometers and perigee 4.8×103 kilometers. The mass
of the satellite in question is 3500 kilograms and the mass of the earth is
5.98×1024 kilograms.
The energy of the circular orbit is given by
E = - 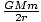 = 9.97×1010
= 9.97×1010 Joules. The equation used here can also be applied to elliptical
orbits with
r replaced by the semimajor axis length
a. The semimajor axis
length is found from
a =  = 5.3×106
= 5.3×106 meters. Then
E = - 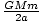 = 1.32×1011
= 1.32×1011 Joules.
The energy of the elliptical orbit is higher.
Problem :
If a comet of mass 6.0×1022 kilograms has a hyperbolic orbit around
the sun of eccentricity
ε = 1.5, what is its closest distance
of approach to the sun in terms of its angular momentum (the mass of the sun is
1.99×1030
kilograms)?
Its closest approach is just
rmin, which is given by:
rmin = 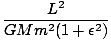 = (6.44×10-67)L2 = (6.44×10-67)L2 |
|