Given a sequence of numbers a1, a2,…, an,… (also denoted simply
{an}), we can form sums:
obtained by summing together the first n numbers in the sequence. We call sn the
nth partial sum of the sequence.
We would like to somehow define the sum of all the numbers in the sequence, if that is
something that makes any sense. We write this sum as
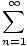 an = a1 + a2 + ... an = a1 + a2 + ... |
|
and call it a series. In many cases, this sum clearly does not make sense--for
example, consider the case where we let each an = 1. As we add more and more of the
an together, the sum gets larger and larger, without bound. In other cases,
however, the sum of all the an seems to make sense. For example, let an = 1/2n.
Then as we begin adding the an together, the sum looks like
As we add on more and more terms, the sum appears to get closer and closer to 1.
Let us make all of this a little more precise. Given a sequence {an}, the partial sums
sn defined above as
form another sequence, {sn}. In our first example above, this sequence of partial
sums looks like
| 1, 1 + 1, 1 + 1 + 1, 1 + 1 + 1 + 1,… |
|
or
In our second example, the sequence of partial sums begins
If the terms of the sequence {sn} gets closer and closer to a particular number as
n→∞, then we say that the series converges to L, or is convergent,
and write
a1 + a2 + ... = 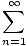 an = an = 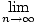 sn = L sn = L |
|
If the sequence of partial sums does not converge to any particular number, then we say
that the series diverges, or is divergent. Hence our first example above diverges and
our second example converges to 1; that is,
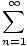 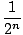 = 1 = 1 |
|
As another example of a divergent series, consider the harmonic series:
To see that this sequence diverges simply note that a2≥1/2, a3, a4≥1/4,
a5, a6, a7, a8≥1/8, etc. Thus,
| s1 | ≥ | 1, |
|
| s2 | ≥ | 1 + 1   , , |
|
| s4 | ≥ | 1 + 1  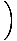 +2 +2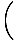 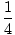 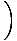 , , |
|
| s8 | ≥ | 1 + 1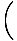  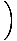 +2 +2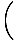 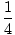 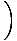 +4 +4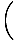 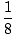 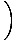 |
|
and so on. We have s2n≥1 + n/2, so the partial sums get arbitrarily large as
n→∞.
We conclude with two basic properties of convergent series. Suppose
 an and
an and  bn are two convergent series. Then
bn are two convergent series. Then
 (an + bn) also converges and
(an + bn) also converges and
Furthermore, if c is a constant, then  can converges and
can converges and
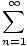 can = c can = c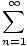 an an |
|