Inverse Functions
Two functions f and g are inverse functions if fog(x) = x and gof (x) = x for all values of x in the domain of f and g.
For instance, f (x) = 2x and g(x) = 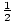 x are inverse functions
because fog(x) = f (g(x)) = f (
x are inverse functions
because fog(x) = f (g(x)) = f (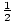 x) = 2(
x) = 2(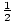 x) = x and gof (x) = g(f (x)) = g(2x) =
x) = x and gof (x) = g(f (x)) = g(2x) = 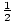 (2x) = x. Similarly, f (x) = x + 1
and g(x) = x - 1 are inverse funcions because fog(x) = f (g(x)) = f (x - 1) = (x - 1) + 1 = x and gof (x) = g(f (x)) = g(x + 1) = (x + 1) - 1 = x.
h(x) = 3x - 1 and j(x) =
(2x) = x. Similarly, f (x) = x + 1
and g(x) = x - 1 are inverse funcions because fog(x) = f (g(x)) = f (x - 1) = (x - 1) + 1 = x and gof (x) = g(f (x)) = g(x + 1) = (x + 1) - 1 = x.
h(x) = 3x - 1 and j(x) = 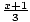 are inverse functions because hoj(x) = h(j(x)) = h(
are inverse functions because hoj(x) = h(j(x)) = h(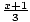 ) = 3(
) = 3(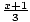 ) - 1 = x + 1 - 1 = x and joh(x) = j(h(x)) = j(3x - 1) =
) - 1 = x + 1 - 1 = x and joh(x) = j(h(x)) = j(3x - 1) = 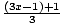 =
= 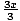 = x.
= x.
The inverse of a function f (x) is denoted f-1(x).
Finding the Inverse of a Function by Reversing Operations
The trick to finding the inverse of a function f (x) is to "undo" all the
operations on x in reverse order.
The function f (x) = 2x - 4 has two steps:
- Multiply by 2.
- Subtract 4.
Thus,
f-1(x) must have two steps:
- Add 4.
- Divide by 2.
Consequently,
f-1(x) = 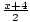
.
We can verify that this is the inverse of
f (x):
f-1(f (x)) = f-1(2x - 4) = 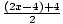 =
= 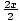 = x.
= x.
f (f-1(x)) = f (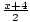 ) = 2(
) = 2(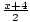 ) - 4 = (x + 4) - 4 = x.
) - 4 = (x + 4) - 4 = x.
Example 1: Find the inverse of f (x) = 3(x - 5).
Original function:
- Subtract 5.
- Multiply by 3.
New function:
- Divide by 3.
- Add 5.
Thus,
f-1(x) = 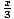 + 5
+ 5.
Check:
f-1(f (x)) = f-1(3(x - 5)) = 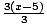 + 5 = (x - 5) + 5 = x.
+ 5 = (x - 5) + 5 = x.
f (f-1(x)) = f (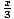 +5) = 3((
+5) = 3((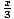 +5) - 5) = 3(
+5) - 5) = 3(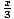 ) = x.
) = x.