payment page
-
Acute Angle
An angle with a measure of less than 90 degrees.
-
Addition Properties of Inequality
If a < b, then a + c < b + c
If a > b, then a + c > b + c -
Greater Than
a > b if and only if there is a positive number c such that a - c = b.
-
Inequality
A statement that shows the relationship between two (or more) expressions with one of the following five signs: <, ≤, >, ≥, ≠.
-
Inequality Properties of Opposites
If a > 0, then - a < 0
If a < 0, then - a > 0 -
Less Than
a < b if and only if there is a positive number c such that a + c = b.
-
Multiplication and Division Properties of Inequality
For positive numbers:
If a < b and c > 0, then ac < bc and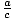
< 
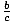
If a > b and c > 0, then ac > bc and >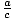
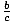
For negative numbers:
If a < b and c < 0, then ac > bc and >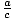
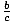
If a > b and c < 0, then ac < bc and <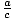
-
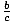
Obtuse Angle
An angle with a measure greater than 90 degrees, but not more than 180 degrees.
-
Property of Squares of Real Numbers
a2≥ 0 for all real numbers a.
-
Right Angle
An angle with a measure of exactly 90 degrees.
-
Subtraction Properties of Inequality
If a < b, then a - c < b - c
If a > b, then a - c > b - c -
Transitive Properties of Inequality
If a < b and b < c, then a < c.
If a > b and b > c, then a > c. -
Trichotomy Property
For any two real numbers a and b, exactly one of the following is true: a < b, a = b, a > b.
