Equilibrium

The Graphical Approach

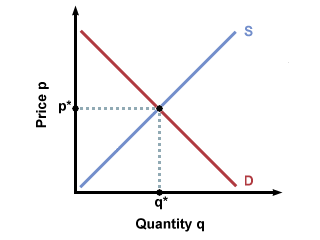
By now, we are familiar with graphs of supply curves and demand curves. To find market equilibrium, we combine the two curves onto one graph. The point of intersection of supply and demand marks the point of equilibrium. Unless interfered with, the market will settle at this price and quantity. Why is this? At this point of intersection, buyers and sellers agree on both price and quantity. For instance, in the graph below, we see that at the equilibrium price p*, buyers want to buy exactly the same amount that sellers want to sell.

If the price were higher, however, we can see that sellers would want to sell more than buyers would want to buy. Likewise, if the price were lower, quantity demanded would be greater than quantity supplied. The following graph shows the discrepancy in supply and demand if the price is higher than the equilibrium price:

Note that the quantity that sellers are willing to sell is much higher than the quantity that buyers are willing to buy.

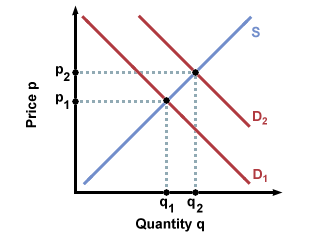
We can also see what happens when one of the curves shifts up or down in response to outside factors. For example, if we were to look at the market for Beanie Babies before and after they became a popular fad, we would see a shift outwards from the initial demand curve over time. The reason for this is that as people began to like Beanie Babies, their preferences changed, and they began to want Beanie Babies enough that they would pay much more for each Beanie Baby than they would have previously. We can see this new preference for Beanie Babies in the outward shift of the demand curve: for every price, buyers will buy more Beanie Babies than they would have before the fad.

Note that this combines two effects we studied earlier: there is a shift in the demand curve, which causes a movement up the supply curve. These two effects combine to reach the new market equilibrium, which has both a higher price and a higher quantity than the previous market equilibrium.

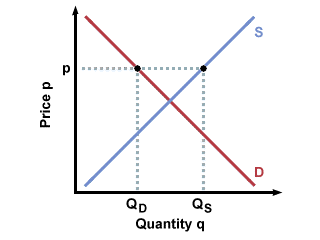
It is only through a shift in either the supply or the demand curve that the market equilibrium will change. Why is this? If neither curve shifts, and we move along one of the curves, the market will naturally shift back to equilibrium. For example, if we look at a market in equilibrium, and a store tries to move up its supply curve by selling goods at a higher price, the result will be that no one will buy the goods, since they are less expensive at the store's competitors. The store will have to either go out of business, or move its prices back down to equilibrium.

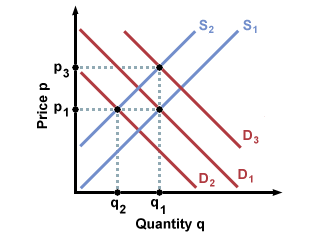
What happens if both curves shift? Will we end up at the same equilibrium point? In this model, it is not possible to reach the same equilibrium: either the price or the quantity can be the same as the previous equilibrium, but not both, unless the curves shift back to their original positions. To illustrate why this is true, consider the graph below. The initial equilibrium, between supply curve 1 and demand curve 1, has price p* and quantity q*. If supply shifts to supply curve 2, both equilibrium price and quantity change. It is now possible to change back to our original price by shifting the demand curve to position 2 or it is possible to revert to our original quantity by shifting the demand curve to position 3. Note that we cannot reach the original equilibrium point unless we move the curves back to their original points.

For a real world example, consider the market for oil. The initial supply and demand curves would be at position 1 (p1). When the suppliers decide to collaborate and supply less oil for every price, this causes a backwards shift in the supply curve, to supply curve 2. This cuts the quantity supplied from quantity 1 (q1) to quantity 2 (q2) and raises the price paid for oil along demand curve 1. We can either shift the demand curve in to curve 2, maintaining previous price levels, but decreasing consumption even more, or we can shift our demand curve out to curve 3, maintaining previous levels of consumption but raising prices. Since there is a tradeoff between having steady prices or steady consumption, the consumers have to make a decision about which is more important to them. In the short run, they will probably decide to pay the higher prices to keep consumption steady (that is, they will shift out to curve 3), but if the prices stay high for a long time, they will start finding ways to economize, (thereby shifting in to curve 2).

The Algebraic Approach

We have worked with supply and demand equations separately, but they can also be combined to find market equilibrium. We have already established that at equilibrium, there is one price, and one quantity, on which both the buyers and the sellers agree. Graphically, we see that as a single intersection of two curves. Mathematically, we will see it as the result of setting the two equations equal in order to find equilibrium price and quantity.

If we are looking at the market for cans of paint, for instance, and we know that the supply equation is as follows:

QS = -5 + 2P

And the demand equation is:

QD = 10 - P

Then to find the equilibrium point, we set the two equations equal. Notice that quantity is on the left-hand side of both equations. Because quantity supplied is equal to quantity demanded at equilibrium, we can set the right-hand sides of the two equations equal.

QS = QD
-5 + 2P = 10 - P
3P = 15
P = 5

At equilibrium, paint will cost $5 a can. To find out the equilibrium quantity, we can just plug the equilibrium price into either equation and solve for Q.

Q* = QS
QS = -5 + 2(5)
QS = Q* = 5 cans

Shifts up and down supply and demand curves are represented by plugging different prices into the supply and demand equations: different prices yield different quantities. For example, changing the price to $6 a can would decrease quantity demanded from 5 cans to 4 cans, as we can see when we plug the two prices into the demand function:

P = 5
QD = 10 - 5 = 5 cans

P = 6
QD = 10 - 6 = 4 cans

The equivalent of shifting supply and demand curves is changing the actual supply and demand equations. Let's say that everyone in a small town just recently painted their houses, and therefore no longer need any paint. This means that they will be less willing to buy paint, even if the price doesn't go up. Their new demand function might be:

QD = 7 - P

We can see that for any price, they will demand fewer cans of paint. At the old equilibrium price of $5, they will only buy:

QD = 7 - 5 = 2 cans of paint

This new equation, representing a shift in demand, also causes a shift in market equilibrium, which we can find by setting the new demand equation equal to supply:

QS = QD
-5 + 2P = 7 - P
3P = 12
P = $4 a can

Now to solve for the equilibrium quantity:

Q* = QS
QS = -5 + 2P = -5 + 2(4)
QS = Q* = 3 cans of paint

At the new equilibrium, 3 cans of paint will be sold at $4 each.