Organic Chemistry: Enantiomers and Diastereomers: Enantiomers

Chirality

In the previous chapter we defined stereoisomers as molecules that have the same connectivity but differ in their spatial arrangement of atoms. We saw that the rigidity of double bonds gave rise to one type of stereoisomerism, cis-trans isomerism. However, it turns out, cis-trans isomers form only a small subset of stereoisomers. A more important type of stereoisomerism arises from molecules that are chiral.

You already have some intuitive notion of what it means for an object to be chiral, which is a Greek word meaning "handed". Consider the relation between your left and right hands. They appear to be the same, and yet there are clearly some ways in which they are distinct. For example, a right glove that fits easily over your right hand will not fit over your left hand. You would have a hard time fitting a left shoe over your right foot. A pair of right-handed scissors works fine in your right hand but feels awkward when you try to use your left hand.

What does it mean for an object to be chiral? To answer this question, again consider your left and right hands. The objects look identical; in fact theyare mirror images of each other. However, they are not the same. The test used to determine whether two objects are identical is superimposability. That is, can two objects be placed in the same space in such a way that all of their components overlap? Try the test of superimposability on your left and right hands, and you should see that they are not superimposable. This allows us to define what it means for an object to be chiral:

a chiral object is one that is not superimposable on its mirror image.

Conversely, an achiral object is one that is identical (superimposable) to its mirror image.

How can we tell whether a given object is chiral? The most straightforward way to determine whether a given object is chiral is to draw or visualize the object's mirror image and see if the two are identical (that is, superimposable). If the object contains an internal plane of symmetry then it must be achiral. However, as we shall see, the converse is not true: an object that has no internal plane of symmetry may also be achiral.

Chiral Molecules

Molecules, like other objects, can be chiral or achiral. For example, build a model of 2-butanol (butane with an -OH substituent on the second carbon) and its mirror image:

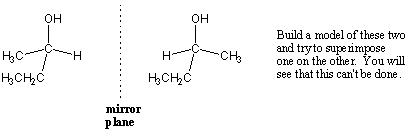
Figure %: The mirror images of 2-butanol

Try to physically superimpose these models and you'll see that they're not superimposable. This means that there are two distinct versions of 2-butanol, a right-handed one and a left-handed one. Each version of 2-butanol is a chiral molecule. What is the relation between them? The two molecules are clearly isomers, and since they have the same atomic connectivities they are stereoisomers. Unlike cis-trans isomerism, this stereoisomerism arises from the ability of molecules to be chiral. A chiral molecule and its non-superimposable mirror image are special types of stereoisomers called enantiomers.