Previous Next

Boyle's Law

The most important thing to remember about Boyle's Law is that it only holds when the temperature and amount of gas are constant. A state of constant temperature is often referred to as isothermal conditions. When these two conditions are met, Boyle's law states that the volume V of a gas varies inversely with its pressure P. The equation below expresses Boyle's law mathematically:

PV = C    

C is a constant unique to the temperature and mass of gas involved. plots pressure versus volume for a gas that obeys Boyles law.
Figure %: Pressure versus Volume

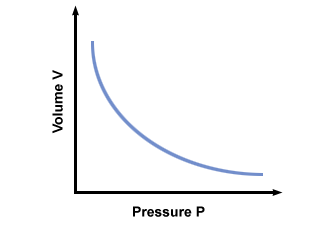
You will get the most mileage out of another incarnation of Boyle's law:

P1V1 = P2V2    

The subscripts 1 and 2 refer to two different sets of conditions. It is easiest to think of the above equation as a "before and after" equation. Initially the gas has volume and pressure V1 and P1. After some event, the gas has volume and pressure V2 and P2. Often you will be given three of these variables and asked to find the fourth. You should realize that this is a simple case of algebra. Separate the knowns and unknowns on two different sides of the "=" sign, plug in the known values, and solve for the unknown.

The Manometer

Boyle used a manometer to discover his gas law. His manometer had an odd "J" shape:

Figure %: A Manometer
As you can see from , there are two ends to Boyle's manometer. One end is open to the atmosphere. The other end is sealed, but contains gas at atmospheric pressure. Since the pressure on both ends of the tube is the same, the level of mercury is also the same.

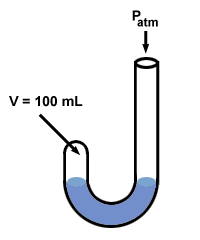
Next Boyle added mercury to the open end of his manometer.

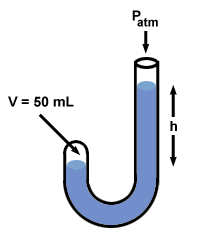
The volume of the gas at the closed end of the manometer decreased, but since gas can't get in or out of the closed end, the amount of gas does not change. Likewise we can assume that the experiment occurs under isothermal conditions. Boyle's law should hold, meaning that the initial volume times pressure should equal the volume times pressure after the additional mercury was added. Let's use the equation below on the gas at the sealed end:

P1V1 = P2V2    

The pressure of the gas before mercury is added is equal to the atmospheric pressure, 760 mm Hg (let's assume that the experiment is run at oC so that 1 torr = 1 mm Hg). So P1 = 760 mm Hg. The volume V1 is measured to be 100 mL.

After Boyle added mercury, the volume of the gas, V2, drops to 50 mL. To find the value of P2, rearrange the equation above and plug in values:


P2=P1V1/V2  
 =(100 mL)(760 mm Hg)/(50 mL)  
 =1520 mm Hg  

If you look back at , you'll notice that the difference P2 - P1 = 760 mm Hg, and that this exactly equals the difference in mercury levels on the two sides, h. In fact, Boyle's manometer illustrates a truism common to all manometers: h corresponds to the difference in pressure between the two ends of the manometer.

Boyle's manometer is only one of the many kinds of manometers you'll face. Don't be disheartened; all manometers are practically the same. Realize that each end of a manometer can only be:

  • sealed and contain a vacuum (P = 0)
  • open to the atmosphere (P = Patm)
  • open to a sample of gas with pressure P
This is the key to solving manometer problems. Once you figure out the pressure at both ends of the manometer, you can use the difference to determine the height h of the liquid column, and vice versa.

Let's try this procedure with a manometer in which one end is open to the atmosphere (760 mm Hg) and the other is sealed off to a vacuum.

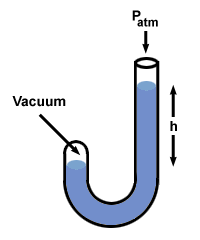
At the end that is sealed off with a vacuum, P = 0 mm Hg. At the end open to the atmosphere, P = 760 mm Hg. The difference between the two pressures is 760 mm Hg, so the height h must correspond to 760 mm Hg, the atmospheric pressure. Thus this manometer has the same function as a barometer; it measures atmospheric pressure.

There are a few other flavors of manometer, but you can handle them if you remember that h is the pressure difference between the two sides of the manometer. Note that the side of the manometer with the highest pressure also has the lowest level of Hg.

Previous section Next section

Take a Study Break